Web page of Ryoko Oishi-Tomiyasu
研究内容
数理結晶学には,調和解析・信号処理・最適化・統計学など様々な手法を用いたアルゴリズム開発としての側面があります.そのため日頃から様々な分野の数学に接するようにしていますが,新しい知見を得るのに数論・代数学といった純粋数学のアイデア・技術を組み合わせることを割とよく行っています.
実施中のプロジェクトに以下のようなものがあります.
-
最近の研究で18世紀から知られる黄金角の方法を一般曲面・一般次元に拡張しました.
古典的な問題によくあるように,得られた理論は学際的な応用があるだけでなく, 代数・幾何・解析の問題(マルコフ理論の高次元化・対角化可能計量を持つ多様体・Lamé偏微分方程式)に横断的に関係しています.
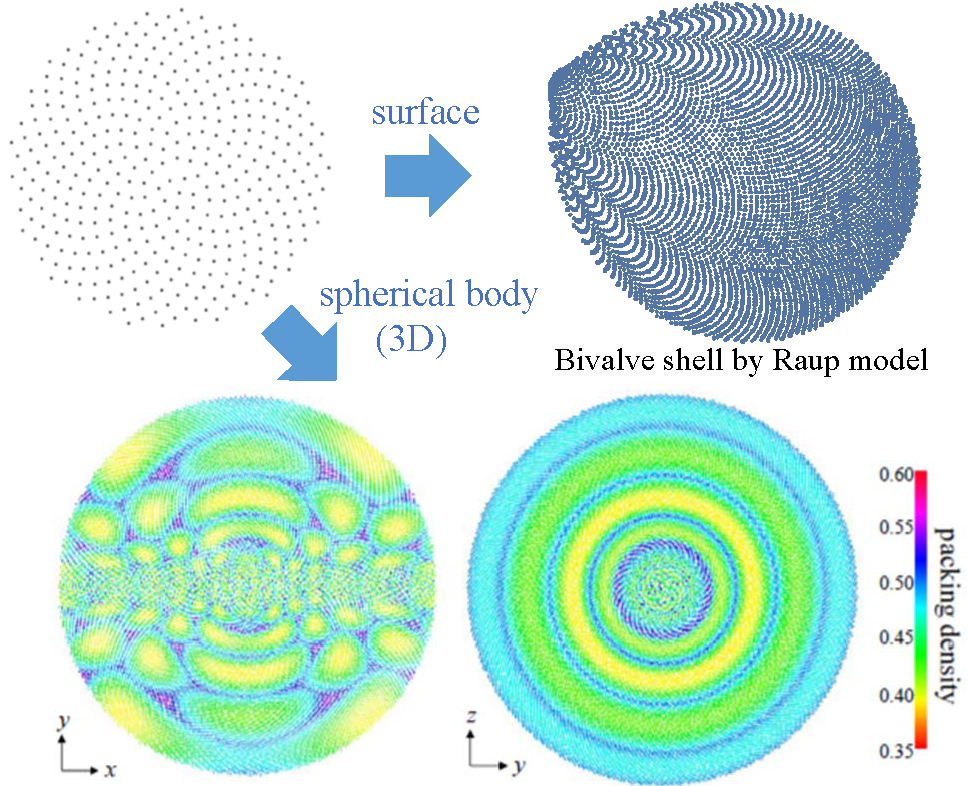
適用結果(3Dは断面図,着色は各点近傍のパッキング密度による)
-
代数計算は整数型などで定義されるexactな数値を主に扱うため, ノイズを含むデータにアプライするには,新しい理論・アルゴリズムの開発が必要となります. 具体的には以下のような問題を扱っています.
- ノイズがある場合の格子の対称性決定
- 回折データ(PXRD, EBSD)からの格子決定アルゴリズム,解の一意性
上記2つの研究では,役に立つ結果が格子基底簡約理論, 群コホモロジー,2次形式のZ上表現論を用いました (最後の項目はKaplansky予想の反例と残る未解決部分にも関係しています).
- 有限データのフーリエ変換に伴う打切り誤差推定法
R^n上フーリエ変換で,得られる観測データが有限な場合の話です.
-
もともと 「位相回復」の数学研究に,私の出身分野である保型形式論が使えないかと思ったのが私が数理結晶学研究を始めたきっかけでした.実際,結晶の単結晶回折・粉末結晶回折データは保型形式の線形和で表すことができます.
この保型形式論の応用は,様々な事情(特に他の研究)からこれまであまり時間をさけてないのですが, 凸最適化を用いた研究として以下を実施しています.
- 凸最適化(半正定値計画緩和法, SDR)を用いた結晶構造・磁気構造解析, 特に大域的最適解の取得
「位相回復」は2次計画問題なので, 問題を適切に設定できればSDRの効率よく大域的最適化を使用でき, 対称性がある場合などに複数の大域的最適解を取得することもできますが(ノイズがある状況での代数計算がここでも必要です), 実験家との共同研究で,結晶・磁気構造解析の状況(正確には,磁気モーメント・原子占有率・原子種の決定)において, 実際にSDRによる大域性の保証が実施できることを示しました.