Web page of Ryoko Oishi-Tomiyasu
My Research
Mathematical crystallography involves algorithm development based on harmonic analysis, signal processing, optimization and statistics, but I often obtain new findings by combining these with ideas and techniques in pure mathematics including algebra and number theory.
The following are the projects I'm primarily conducting.
-
We recently generalized the well-known Gold-angle method so that it can be applied to general surfaces and general dimensions.
As is often the case with classical problems, the developed theory is transversely related to algebra, geometry, analysis (higher dimensional versions of Markoff theory, manifolds with diagonalizable metrics, Lamé partial differential equations) and interdisciplinary applications.
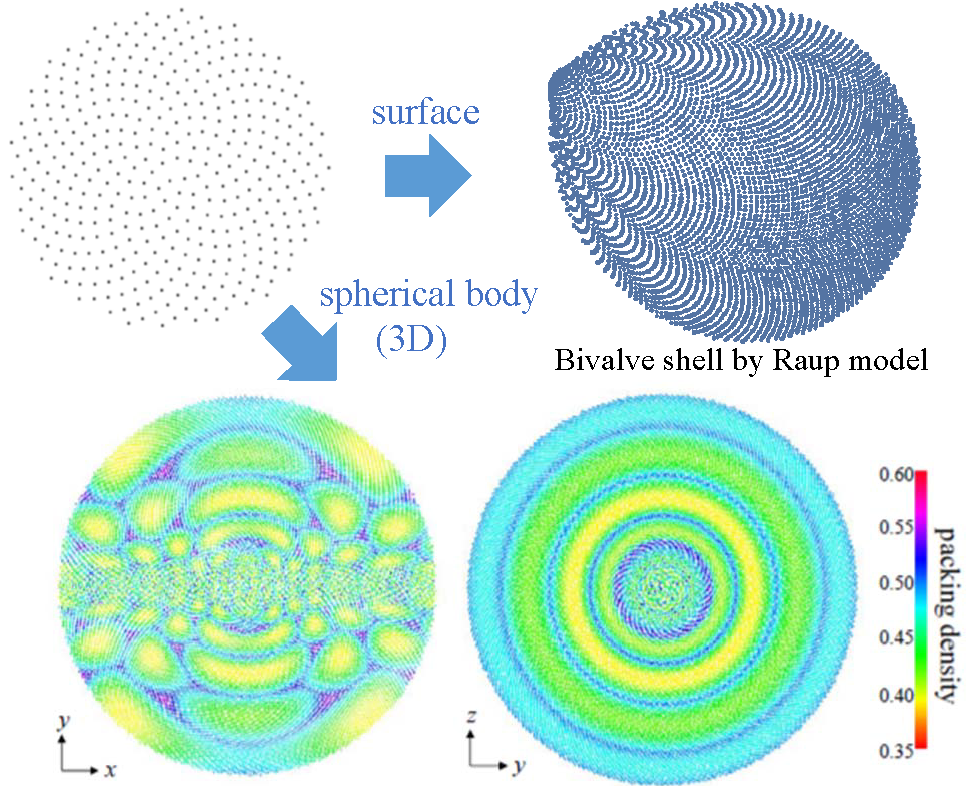
Results(for 3D, cross-sections colored by packing density around each point)
-
The existing methods for algebraic calculation normally assume that all the values are exact (represented by integer types etc.). Therefore, algorithm development is required for noisy data.
Specifically, we have studied the following problems.- Lattice symmetry (Bravais-type) determination robust against observation errors
- Lattice determination (ab-initio indexing) from diffraction patterns (PXRD and EBSD)
For the above two, useful results were obtained by using lattice-basis reduction, group cohomology and representations of quadratic forms over Z (the last one is also related to the counterexamples and still open problems for Kaplansky conjecture).
- Methods for truncated Fourier transform
This concerns the Fourier transform on Rn, where the number of observed data points is finite.
-
- Application of convex optimization (Semidefinite Programming Relaxation, SDR)to assure the global optimality in crystal/magnetic structure analysis
Phase retrieval to determine the amplitudes of the Fourier transform of the crystal structure (=structure factors) can be expressed as a QP. SDR is a method to obtain the global minima of quadratic optimization problems (QP). In a joint work with experimental scientists, we showed that SDR can actually ensure the global optimality in a situation of crystal/magnetic structure analysis (more presicely,in determination of magnetic moment/atomic occupancies/atomic species).